Worker scheduling problem
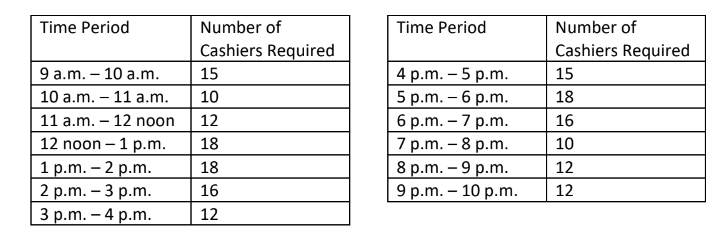
- A grocery store has requirements for between 10 to 18 cashiers depending on the time of day.
- Lunchtime, from noon to 2 p.m., and evening, from 5 p.m. to 6 p.m. are usually busiest.
- The table below indicates the cashiers needed at various hours that the store is open:
- The store now employs 27 full-time cashiers, but many people are on its roster of available part-time employees.
- A part-time employee must put in exactly 4 hours per day but can start anytime between 9a.m. and 6 a.m.
- Part-timers are a fairly inexpensive labour pool because no retirement or lunch/dinner benefits are provided to them. Full-timers, on the other hand, are divided into two groups, one group (i.e. 15 full-timers) works from 9 a.m. to 4 p.m., and the other group (i.e. 12 full-timers) works from 4p.m. to 10 p.m.
- Both group of full-timers are allowed 1 hour for lunch/dinner.
- For the group of full-timers who work from 9 a.m. to 4 p.m., half of the full-timers eat at 11 a.m., and the other half eat at 12noon).
For the group of full-timers who work from 4 p.m. to 10 p.m., half of the full-timers eat at 6 p.m.,and the other half eat at 7 p.m.).
- The store limits part-time hours to a maximum of 50% of the day’s total requirement.
- Part-timers earn RM 7.50 per hour, whereas full-timers earn RM 75 per day.
The management would like to set a schedule the number of full timers and part timers which can minimize the total man-power costs.
Solution
Let
$x_{1}$ = number of full-time cashiers work from 9a.m – 4p.m.
$x_{2}$ = number of full-time cashiers work from 4p.m – 10p.m.
$y_{1}$ = number of part time cashiers start work at 9a.m – 10a.m
$y_{2}$ = number of part time cashiers start work at 10a.m – 11a.m
$y_{3}$ = number of part time cashiers start work at 11a.m – 12noon
$y_{4}$ = number of part time cashiers start work at 12noon – 1p.m
$y_{5}$ = number of part time cashiers start work at 1p.m – 2p.m
$y_{6}$ = number of full-time cashiers work from 2p.m – 3p.m
$y_{7}$ = number of part time cashiers start work at 3p.m – 4p.m
$y_{8}$ = number of part time cashiers start work at 4p.m – 5p.m
$y_{9}$ = number of part time cashiers start work at 5p.m – 6p.m
$y_{10}$ = number of part time cashiers start work at 6p.m – 7p.m
LP formulation
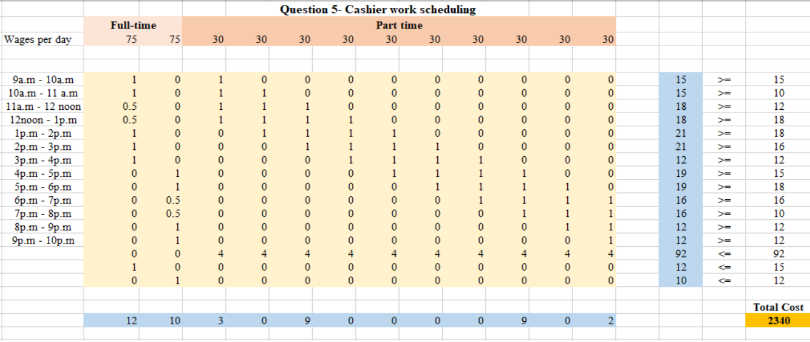
$Min z = 75(x_{1}+x_{2}) + 30(y_{1}+y_{2}+y_{3}+y_{4}+y_{5}+y_{6}+y_{7}+y_{8}+y_{9}+y_{10})$
subject to
$x_{1}+y_{1} \ge 15$ $x_{1}+y_{1}+y_{2} \ge 10$ $1/2x_{1}+y_{1}+y_{2}+y_{3} \ge 12$ $1/2x_{1}+y_{1}+y_{2}+y_{3}+y_{4} \ge 18$ $x_{1}+y_{2}+y_{3}+y_{4}+y_{5} \ge 18$ $x_{1}+y_{3}+y_{4}+y_{5}+y_{6} \ge 16$ $x_{1}+y_{4}+y_{5}+y_{6}+y_{7} \ge 12$ $x_{2}+y_{5}+y_{6}+y_{7}+y_{8} \ge 15$ $x_{2}+y_{6}+y_{7}+y_{8}+y_{9} \ge 18$ $1/2x_{2}+y_{7}+y_{8}+y_{9}+y_{10} \ge 16$ $1/2x_{2}+y_{8}+y_{9}+y_{10} \ge 10$ $x_{2}+y_{9}+y_{10} \ge 12$ $x_{2}+y_{10} \ge 12$ $4(y_{1}+y_{2}+y_{3}+y_{4}+y_{5}+y_{6}+y_{7}+y_{8}+y_{9}+y_{10}) \le 92$ $x_{1} \le 15$ $x_{2} \le 12$
$x_{1},x_{2},y_{1},y_{2},y_{3},y_{4},y_{5},y_{6},y_{7},y_{8},y_{9},y_{10} \ge 0
For the result,they need 12 full-time employee work from 9a.m.-4p.m.
10 full-time employee work from 4p.m to 10p.m.
20 part time cashier should hired
This minimize the total number of full-time cashiers from 27 to 22.
| Period | Full time | Part time |
| 9a.m - 10a.m | 12 | 3 |
| 10a.m - 11a.m | 12 | 3 |
| 11a.m - 12noon | 6 | 12 |
| 12noon - 1p.m | 6 | 12 |
| 1p.m - 2p.m | 12 | 9 |
| 2p.m - 3p.m | 12 | 9 |
| 3p.m - 4p.m | 12 | 0 |
| 4p.m - 5p.m | 10 | 9 |
| 5p.m - 6p.m | 10 | 9 |
| 6p.m - 7p.m | 5 | 11 |
| 7p.m - 8p.m | 5 | 11 |
| 8p.m - 9p.m | 10 | 2 |
| 9p.m - 10p.m | 10 | 2 |