Investment Problem
- A company has scheduled the construction of new plant 5, 10, and 20 years from now.
- To cover at least the construction costs, the CFO needs to invest some of the company’s money to meet future cash-flow needs.
- CFO may purchase only three kinds of financial assets, each of which costs $1 million per unit.
- The assets produce income 5, 10, and 20 years from now, and that income is needed to cover at least minimum cash-flow requirements in those years.
- Any excess income above the minimum requirement for each time period will be used to increase dividend payments to shareholders rather than saving it to help meet the minimum cash-flow requirement in the next time period.
The following table shows both the amount of income generated by each unit of each asset and the minimum amount of income needed for each of the future time periods when a new plant will be constructed.
Determine the mix of investments in these assets that will cover the cash-flow requirements while minimizing the total amount invested.
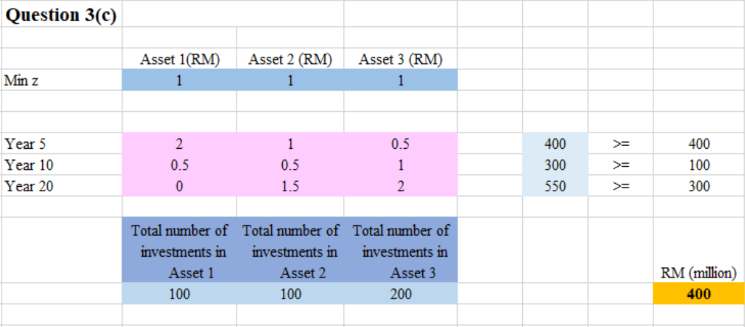
If the CFO purchase 100 units of Asset 1, 100 unit of Asset 2 and 200 units of Asset 3.How much cash flow would this mix of investments generate 5, 10, and 20 years from now?
Solution
Let
$x_{1}$ = the number of investments in Asset 1
$x_{2}$ = the number of investments in Asset 2
$x_{3}$ = the number of investments in Asset 3
LP formulation
$Min z = x_{1} + x_{2} + x_{3}$
subject to
$2x_{1} + x_{2} + 0.5x_{3} \ge 400$
$20.5x_{1} + 0.5x_{2} + x_{3} \ge 100$
$ 1.5x_{2} + 2x_{3} \ge 300$
$x_{1},x_{2},x_{3} \ge 0
If the CFO purchase 100 units of Asset 1, 100 unit of Asset 2 and 200 units of Asset 3.
The company will have RM 400 million cash flow in Year 5, RM 300 million cash flow in Year 10, and RM 550 million cash flow in Year 20